Những 'bí ẩn' trong toán phổ thông: đạo hàm để làm gì?

Bài lược trích của thầy giáo Ngô Minh Đức dưới đây hi vọng sẽ là lời giải thích gần gũi về ý nghĩa và ứng dụng thực tiễn của đạo hàm.

Một năm sau ngày ra trường, bạn đi họp lớp và gặp lại đứa bạn ngồi cùng bàn. Quá bất ngờ vì cô bạn trở nên xinh đẹp, tự tin, khiến bạn phải thốt lên: “Mới có một năm, sao bạn thay đổi nhiều quá vậy?”.

Câu chuyện đơn giản trên đã ẩn chứa ý tưởng đạo hàm trong đó. Khi một điều gì đó thay đổi, nó có thể thay đổi nhanh hay chậm, đạo hàm sẽ cho ta biết “tốc độ thay đổi” của đại lượng đó. Nhờ ý nghĩa này, đạo hàm trở thành công cụ vô cùng quan trọng, ở bất cứ đâu có sự thay đổi, chúng ta sẽ biết được nó thay đổi như thế nào bằng đạo hàm.

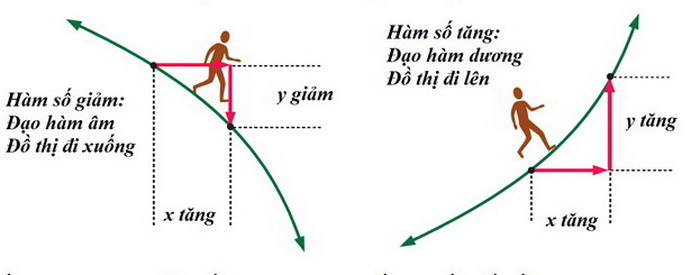
Cụ thể, nếu hàm số đang tăng đạo hàm sẽ dương, tăng càng nhanh thì đạo hàm càng lớn. Ngược lại, hàm số đang giảm, đạo hàm sẽ âm và âm càng nhiều khi hàm số giảm càng nhanh.

Ở khía cạnh thực tiễn, nếu bạn là nhà kinh tế và muốn biết tốc độ tăng trưởng kinh tế nhằm đưa ra những quyết định đầu tư chứng khoán đúng đắn; nếu bạn là nhà hoạch định chiến lược, muốn có thông tin về tốc độ gia tăng dân số ở từng vùng miền; hoặc muốn xác định tốc độ phản ứng hóa học, tính toán tốc độ, gia tốc của chuyển động… Đạo hàm sẽ là thứ mà bạn cần.

Rất đơn giản! Đầu tiên bạn cần có hàm số mô tả đại lượng đang quan tâm và sau đó chỉ cần đạo hàm nó. Còn tính đạo hàm như thế nào thì sách giáo khoa đã chỉ dẫn rõ ràng và chi tiết, đơn giản hơn chúng ta có thể nhờ máy tính làm giúp.

Đạo hàm còn những ứng dụng tuyệt vời khác. Một trong số đó là tìm xem hàm số sẽ đạt được giá trị lớn nhất hay nhỏ nhất ở đâu, để từ đó tối ưu hóa các hoạt động khác nhau trong cuộc sống.

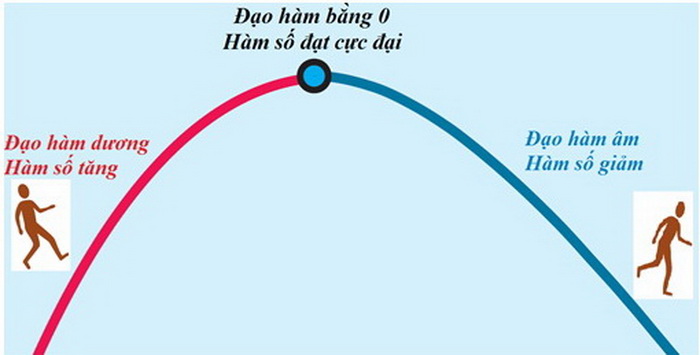
Khi một hàm số đang tăng (đạo hàm dương) rồi bất chợt chuyển sang giảm (đạo hàm âm), nó đã đi qua vị trí mà tại đó hàm số đạt giá trị cực đại và vị trí này cũng chính là nơi có đạo hàm bằng 0 (có thể có ngoại lệ nhé!). Tương tự cho trường hợp hàm số đạt được giá trị cực tiểu.

Từ nhận xét này, bằng cách tìm những chỗ mà đạo hàm bằng 0, người ta có thể biết một đại lượng sẽ đạt giá trị lớn nhất hay nhỏ nhất ở đâu để từ đó có thể tối ưu hóa nó theo mong muốn của mình.

Sử dụng đặc trưng này của đạo hàm, các công ty có thể tính được số sản phẩm nên sản xuất để đạt được lợi nhuận cao nhất. Các kĩ sư sẽ biết phải thiết kế một hộp sữa hay một lon nước ngọt như thế nào, với lượng nguyên liệu có sẵn, để có một hộp sữa chứa được nhiều sữa nhất…

Cụ thể, ta cần có hàm số mô tả lợi nhuận theo số lượng sản phẩm hoặc hàm số mô tả thể tích hộp sữa theo kích thước thiết kế. Đạo hàm sẽ giúp ta tìm xem các hàm số này đạt giá trị lớn nhất tại đâu. Đó chính là lựa chọn tối ưu cho nhà sản xuất.

Ở các sách giáo khoa nước ngoài, họ luôn nhấn mạnh cho học sinh rằng ý nghĩa quan trọng nhất của đạo hàm là cho biết tốc độ thay đổi (rate of change) của một hàm số.

Reference

• Những ‘bí ẩn’ trong toán phổ thông: đạo hàm để làm gì?, https://tuoitre.vn/nhung-bi-an-trong-toan-pho-thong-dao-ham-de-lam-gi-2017101215393784.htm